GeoGebra: Kongruenzsätze am Dreieck

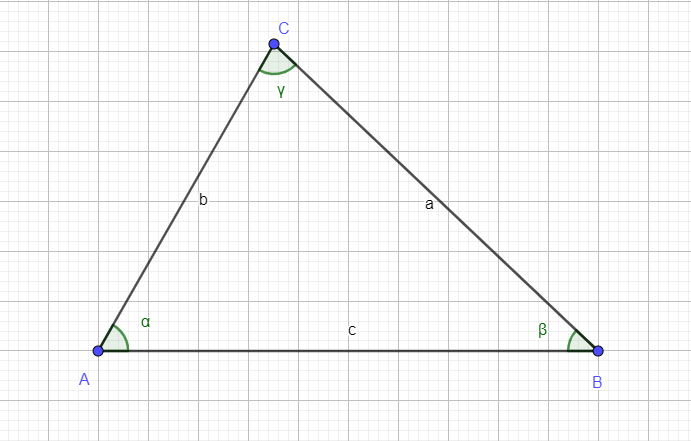
Die Punkte eines Dreiecks werden mit Großbuchstaben benannt. Den Punkt A kann man beliebig setzen. Danach erfolgt die Beschriftung der Punkte in alphabetischer Reihenfolge gegen den Uhrzeigersinn. Gegenüber dem Punkt A liegt die Seite a, gegenüber dem Punkt B die Seite b, und gegenüber dem Punkt C die Seite c. Die Seiten eines Dreiecks werden mit Kleinbuchstaben benannt. Die Winkel werden mit kleinen griechischen Buchstaben bezeichnet. Ein Winkel wird immer nach dem Punkt, an dem er liegt, benannt. Das heißt, im Punkt A liegt der Winkel α, im Punkt B der Winkel β, und im Punkt C der Winkel γ.

Damit wir ein Dreieck konstruieren können, müssen noch einige Gegebenheiten beachtet werden:

1. Drei Punkte, die nicht auf einer Gerade liegen, lassen sich zu einem Dreieck verbinden.
2. In jedem Dreieck ist die Summe zweier Seitenlängen stets größer als die dritte Seitenlänge.
3. In jedem Dreieck beträgt die Summe der Innenwinkel  (Innenwinkelsummensatz).
4.In jedem Dreieck beträgt die Summe der Außenwinkel  (Außenwinkelsummensatz).
5. Ein Außenwinkel ist so groß wie die Summe der beiden nicht anliegenden Innenwinkel (Außenwinkelsatz).
6. In jedem Dreieck liegt der größte Winkel der größten Seite gegenüber.
7. Gleich langen Seiten liegen gleich große Winkeln gegenüber.
8. Gleich großen Winkeln liegen gleich lange Seiten gegenüber.

Um ein bestimmtes Dreieck konstruieren zu können, müssen wir  drei Größen des Dreiecks kennen und einen der vier Kongruenzsätze anwenden können, um ein bestimmtes Dreieck konstruieren zu können.

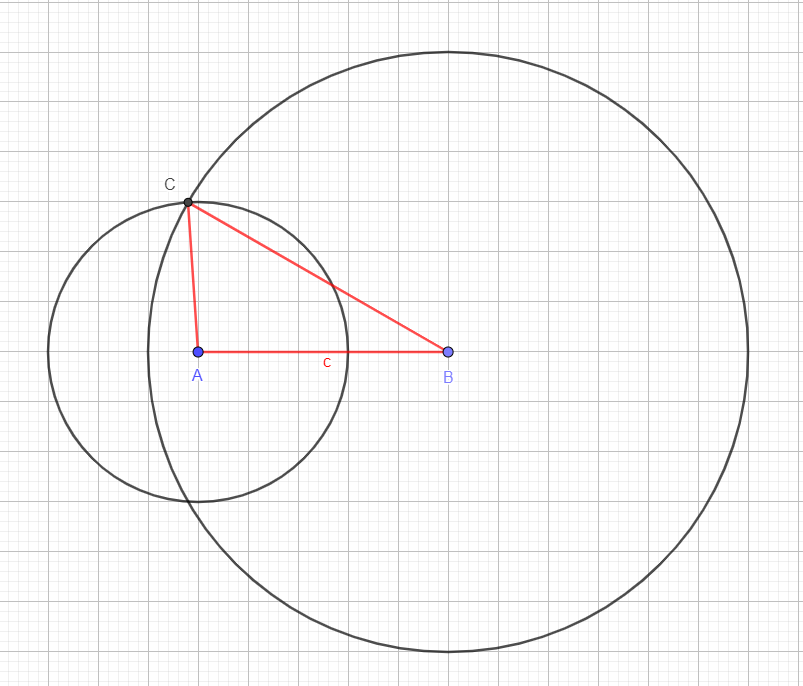
1. Kongruenzsatz (SSS)

Ein Dreieck kann eindeutig konstruiert werden, wenn die Längen aller drei Seiten bekannt sind. Zu beachten ist, dass die Summe zweier Seitenlängen größer als die dritte Seitenlänge ist.

Konstruktion: z.B. a=6 , b=3, c=5

1. Man zeichnet eine Seite mit ihrer gegebenen Länge und zeichnet die Endpunkte ein. (z.B. c mit den Punkten A und B)
2. Man zeichnet um den einen Streckenpunkt einen Kreis mit dem Radius der anliegenden Seite (z.B. Kreis um A mit Radius b)
3. Man zeichnet um den anderen Streckenpunkt einen Kreis mit dem Radius der anderen anliegenden Seite (z.B. Kreis um B mit Radius a).
4. Der Schnittpunkt der beiden Kreise ist der dritte Dreieckspunkt (hier C).
5. Man verbindet die Punkte untereinander.

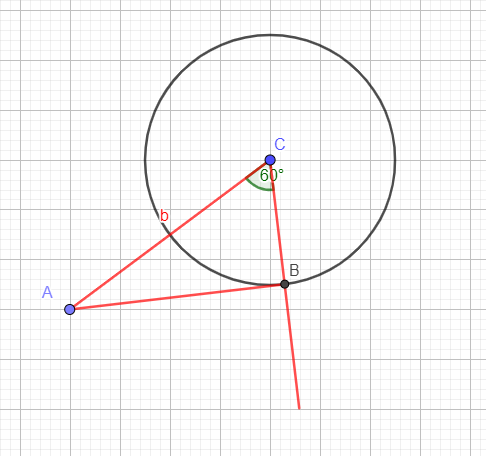
2. Kongruenzsatz (SWS)

Ein Dreieck kann eindeutig konstruiert werden, wenn zwei Seiten und der zwischen den beiden Seiten liegende Winkel bekannt ist.

Konstruktion: a=2,5, γ=60°, b=5

1. Man zeichnet eine Seite mit ihrer gegebenen Länge und zeichnet die Endpunkte ein (z.B. b mit A und C)
2. Man trägt den gegebenen Winkel am richtigen Punkt an und enthält eine Halbgerade. (y in C an b)
3. Man zeichnet einen Kreis um den Winkelpunkt mit dem Radius der zweiten bekannten Seite (Kreis um C mit a)
4. Der Schnittpunkt des freien Schenkels mit dem Kreis ist der dritte Dreieckspunkt (Schnittpunkt B)

3. Kongruenzsatz (WSW)

Ein Dreieck kann eindeutig konstruiert werden, wenn eine Seite und ihre angrenzenden Winkel bekannt sind.

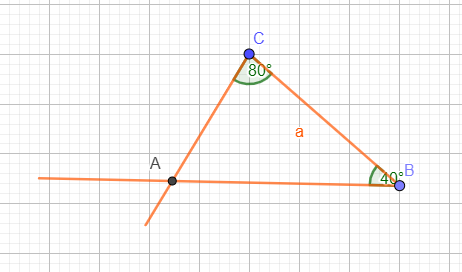
Konstruktion: a=4, β=40°, γ=80°

1. Man zeichnet die gegebene Seite mit ihren Endpunkten (hier: a mit B und C)
2. Man trägt in den beiden Endpunkten jeweils die zughörigen Winkel an (in B b und in C y)
3. Der Schnittpunkt der freien Schenkel ist der gesuchte dritte Eckpunkt (A)

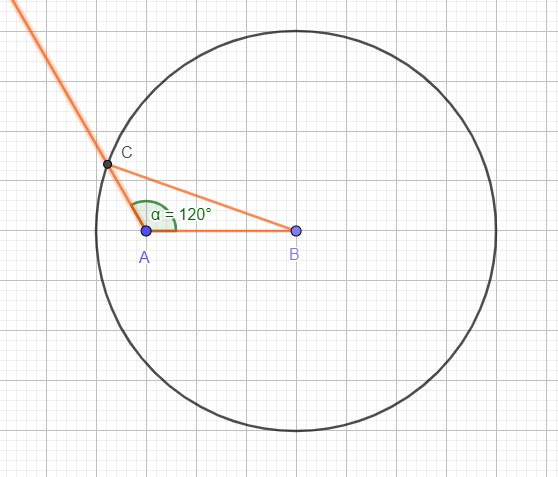
4. Kongruenzsatz (SsW)

Ein Dreieck kann eindeutig konstruiert werden, wenn zwei Seiten und ein angrenzender Winkel gegeben sind. Der Winkel muss der größeren Seite gegenüber liegen

Konstruktion: a=4, c=3, α=120°

1. Man zeichnet die Seite, an der der Winkel angrenzt (hier: c mit den Punkten A und B)
2. Man legt den Winkel am richtigen Punkt an. (hier: α in A)
3. Man zeichnet einen Kreis um den anderen Punkt mit der dem Winkel gegenüberliegenden Seite (Kreis um B mit a)
4. Der Schnittpunkt von freiem Schenk und Kreis ist der gesuchte Dreieckspunkt ( C)