Projekte
Grashalme
Mit Hilfe eines Zollstockes kann man das Wachstum eines Halmes simulieren. Ein Zollstockglied stellt einen Teil des Halmes dar. Seine Auslenkung nach links oder rechts schwankt um einige Grad. Folgende Parameter können zum Testen benutzt werden:
| Anzahl der Glieder | Gliedlänge | Schwankung | Anzahl Zollstöcke |
|---|---|---|---|
| 5 | 40 | 10, 20, 50 | 30 |
| 20 | 10 | 5, 15, 40 | 30 |
| 100 | 2 | 1, 3, 7 | 30 |
Stempeln
Ziel des Projektes ist, ein Software-Paket zu erstellen, mit dem man auf dem Bildschirm Ansichten von Gebäuden entwerfen kann.
Die einzelnen Kostüme werden z.B. den Zifferntasten zugeordnet. Um sie punktgenau ins Bühnenbild setzen zu können, wird die Mausposition gerastert, d.h., das Bild richtet sich an einem Raster aus. Damit nicht für jedes Kostüm ein eigenes Skript geschrieben werden muss, wird auf die Möglichkeit zurückgegriffen, dass ein Abdruck hinterlassen werden kann. Das Hauptprogramm ist oben angegeben, die benötigten Blocks und Tastenaufrufe sind nicht vollständig und müssten ergänzt werden. Man kann natürlich auch eigene Vorschläge entwickeln.
Lissajoufiguren
Lissajous-Figuren sind Kurvengraphen, die durch die Überlagerung
zweier harmonischer, rechtwinklig zueinander stehender Schwingungen
verschiedener Frequenz entstehen. Sie sind benannt nach dem
französischen Physiker Jules Antoine Lissajous (1822–1880). Eine
Lissajous-Figur ist der Graph, der durch die Parametergleichungen
x=a1sin(b1t+c1)
y=a2sin(b2t+c2)
beschrieben wird. In Anlehnung an
die harmonische Schwingung heißen die Größen ai Amplituden, bi
Kreisfrequenzen und ci Phasen (i=1, 2). Typische Lissajous-Figuren
erhält man über die vereinfachten Gleichungen x=sin(b1t) /\ y=sin(b2t).
Die Variablen b1 und b2 stehen für natürliche Zahlen. Tritt zwischen
den beiden Sinusfunktionen zu einer Grundfigur eine "Phasenverschiebung"
c1-c2 auf, so geht eine Symmetrie verloren. Die Graphen verändern sich
je nach Phasenlage, bewahren aber ihr Grundaussehen. Im vorliegenden
Programm erfolgt die Phasenverschiebung kontinuierlich, so dass man den
Eindruck einer sich drehenden Kurve hat.
Taschenrechner
Einmaleins
Je nach Bedarf: das kleine oder große Einmaleins zum Lernen. Die richtigen Ergebnisse werden samt Gleichung eingetragen, die falschen ohne Ergebnis.
Logik
Das folgende Beispiel zeigt Wahrheitstafeln und zeigt die Wirkung von Werten bei Vergleichen.
Partyprobleme
Michaela schreibt Einladungen für ihre Geburtstagsfeier. Dabei hat sie Probleme. Sylvia hatte vor einigen Tagen Streit mit Monika und will auf keinen Fall kommen, wenn Monika auch eingeladen wird. Karin und Anette sind in letzter Zeit unzertrennliche Freundinnen. Sie kommen beide oder gar nicht. Beate, Monika und Karin sollen auch nicht zusammen eingeladen werden, sondern nur zwei von den dreien. Wen muss Michaela einladen, um möglichst viele ihrer Freundinnen bei sich zu haben? Solche Logikaufgaben findet man häufig auf Rätselseiten. Wie kann die Lösung mit Hilfe von Scratch finden?
Zunächst werden die oben angegebenen Probleme als Aussagen Formuliert:
A := ¬Monika ∨ ¬Sylvia
B := (Karin ∧ Anette) ∨ (¬Karin ∧ ¬Anette)
C
:= (Beate ∧ Monika ∧ ¬Karin) ∨ (Beate ∧ ¬Monika ∧ Karin) ∨ (¬Beate ∧ Monika ∧
Karin)
D := A ∧ B ∧ C
In fünf ineinander geschachtelten Schleifen werden alle möglichen Personenkombinationen zusammengestellt und anschließend getestet, ob die Aussagen wahr sind. Sind sie wahr, wird das entsprechende Ergebnis in eine Liste eingetragen. Nach Durchlauf der innersten Schleife wird eine Linie in die Liste eingetragen. Anschließend sucht man sich das Päckchen mit den meisten Namen.
Aufgrund des relativ langen Programm befindet sich hier eine Downloadmöglichkeit: Partyprobleme
Polyturtle
Eine Polyturtle ist ein Gebilde, das aus mehreren unabhängig voneinander operierenden Turtles besteht. In dem folgenden Beispiel sitzen die Turtles in den Ecken eines Quadrates. Auf ein Kommando hin starten sie zur Verfolgungsjagd; T1 läuft hinter T2, T2 hinter T3, T3 hinter T4 und T4 hinter T1 her. Das Programm wird dahingehend verändert, dass zwischen der Position der Schildkröte und ihres Ziels die Verbindungsstrecke gezeichnet wird. Das Programm lässt sich weiter abändern. T1 verfolgt im ersten Lauf T2, T2 T3 usw. In einem zweiten Lauf verfolgt T1 T4, T4 T3 usw. Man kann auch die Zahl der Turtle erhöhen.

Hangman
Fischen
Der Fischteich: ein biologisches System. Im Fischteich befinden sich Friedfische und Raubfische. Die friedlichen Fische ernähren sich von den im Teich anzutreffenden Pflanzen und Futter des Züchters, während die Raubfische die Friedfische fressen. Der Teich bietet Platz für 3000 Friedfische. Im ersten Beispiel sollen 200 Friedfische den Teich bevölkern; die Raubfische haben noch keine Bedeutung. In jeder Periode vermehren sich die Friedfische um 8%, während 2% von ihnen sterben.
Zustandsgleichungen
Fische. Neu
<-- Fische.alt + dt*(ZuFische-AbFische)
Startwert Fische = 200
Zustandsänderungen
ZuFische =
GeburtenFische
AbFische = ToteFische
Konstanten
Zwischenwerte
GeburtenFische =
Fische*0,08
ToteFische= Fische*0,02
In dieser Simulation wird schnell klar, dass es zu einem exponentiellen Wachstum kommt. Im zweiten Beispiel wird die Vermehrung der Fische durch die Kapazität des Teiches beschränkt. Die Geburtenrate wird durch einen Faktor ergänzt, der abhängig von der Kapazität des Teiches ist.
Ein Wachstumsvorgang, der durch einen begrenzenden Faktor eingeschränkt wird, heißt logistisches Wachstum.
Zustandsgleichungen
Fische.neu
<-- Fische.alt + dt*(ZuFische-AbFische)
Startwert Fische = 200
Zustandsänderungen
ZuFische =
GeburtenFische
AbFische = ToteFische
Konstanten
MaxFisch = 3000
Zwischenwerte
Geburtenrate =
0,08*(MaxFisch-Fische)/1000
GeburtenFische = Fische*Geburtenrate
ToteFische= Fische*0,02
In einer weiteren Simulation sollen folgende Vorgaben gemacht werden:
- Im Fischteich sind 2700 Fische.
- Das Fangziel des Anglers liegt bei maximal 200 Fischen pro Periode.
- Sinkt der Bestand auf weniger als 10% der Teichkapazität, ist das Fangergebnis vom Zufall abhängig
- Das Teichfassungsvermögen liegt bei 3000 Fischen.
Zustandsgleichungen
Fische.neu
<-- Fische.alt + dt*(ZuFische-AbFische)
Startwert Fische = 2700
Zustandsänderungen
ZuFische =
GeburtenFische
AbFische = ToteFische + Angler
Konstanten
Teichfassungsvermögen =
3000
Fangziel = 200
Zwischenwerte
GeburtenFische =
Fische*0,08*(FMax-Fische)/1000
ToteFische= Fische*0,02
Angelbeschränkung = FMax/10
Angler = Wenn (Fische >
Angelbeschränkung)
Dann Angler = 200
Sonst Wenn (Fische > Fangziel)
Dann Angler ) Zufall(Fangziel)
Sonst Angler = Zufall (Fische/10)
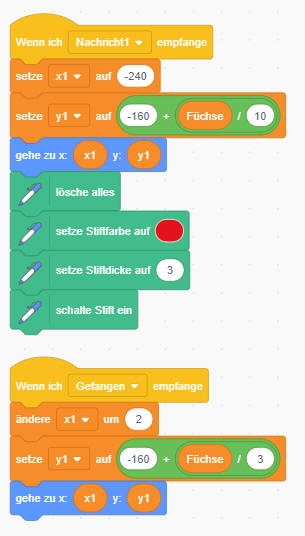
Hasen
Die in einem bestimmten Gebiet vorhandene Weidefläche lässt (bei Abwesenheit von Räubern) den Bestand der beute (hier Hasen) bis an die Grenze der Weidekapazität wachsen. Räuber (hier Füchse) verringern jedoch den Beutebestand entsprechend der Häufigkeit des Zusammentreffens zwischen Beute und Räuber, die vom Bestand der beiden Populationen abhängt. Ohne Beute verhungert der Räuber.
Folgende Modellgleichungen werden angenommen (sie können natürlich variiert werden):
Zustandsgleichungen
Hasen.neu
<-- Hasen.alt + dt*(Hasenzuwachs-Hasenabnahme)
Startwert Hasen = 200
Fuechse.neu <-- Fuechse.alt + dt*(Fuchszunahme-Fuchsabnahme)
Startwert Füchse = 50
Zustandsänderungen
Hasenzuwachs =
0.001*Hasen*freieWeide*Hasenzuwachsrate
Hasenabnahme = 0.002*Treffen
Fuchszunahme = 0.0004*Treffen
Fuchsabnahme = Energieverlust*Füchse
Konstanten
Energieverlust = 0.2
Hasenzuwachsrate = 0.08
Weidekap = Wenn(Zeit<100;2000;500)
Zwischenwerte
Treffen =
Hasen*Füchse
freieWeide = Weidekap-Hasen
Es werden zwei Objekte benötigt: Hasen und Füchse.
Radioaktiver Zerfall
Eine radioaktive Substanz zerfällt in eine Tochtersubstanz und diese wiederum in ein stabiles Endprodukt. Für jede Substanz wird die prozentual vorhandene Restmasse über die Zerfallszeit angezeigt. Dazu werden drei Zeichenobjekte gebraucht, die jeweils eigene Skripts haben. Diese werden über ein Hauptskript angesprochen. Dieses Hauptskript kann bei einem Zeichenobjekt eingerichtet werden (das ist hier der Fall), es könnte aber auch als Skript der Bühne formuliert werden.
