Qualifikationsphase 2
Erkennende Automaten
Echelon ist der Name eines Spionagenetzes. Zunächst war es nur
dazu gedacht, die militärische und diplomatische Kommunikation der
Sowjetunion und ihrer Verbündeten abzuhören. Heute wird das System zur
Suche nach terroristischen Verschwörungen, Aufdeckungen im Bereich
Drogenhandel und als politischer und diplomatischer Nachrichtendienst
benutzt. Seit Ende des Kalten Krieges dient dieses System auch der
Wirtschaftsspionage. Das Echelon-System ist im Aufbau einfach. Die
Mitgliedsstaaten stellen Abhörstationen und Weltraumsatelliten auf, um
Satelliten-, Mikrowellen- und Mobilfunk-Kommunikation abzuhören. Die
eingefangenen Signale werden durch eine Reihe Supercomputer verarbeitet,
die darauf programmiert wurden, Zieladressen, Wörter, Sätze oder sogar
individuelle Stimmen zu erkennen. Dabei ist es mittlerweile sogar
möglich, nach ganzen Sachverhalten zu suchen und nicht nur nach
einzelnen Schlagwörtern.
Erkennende Automaten sind Maschinen, die Zeichenfolgen analysieren. Sie
produzieren keine Ausgaben.
Für drei Beispielen sollen erkennende Automaten entwickelt werden:
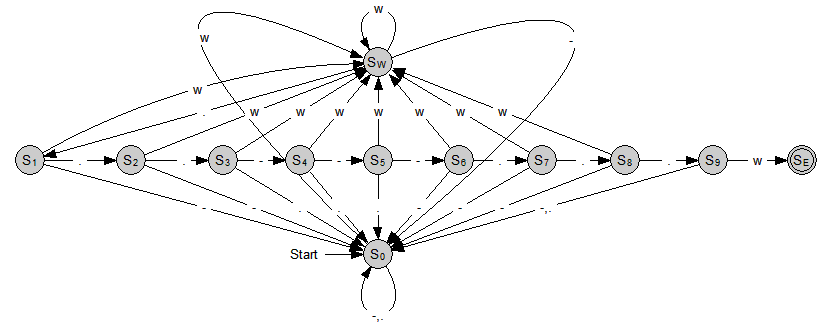
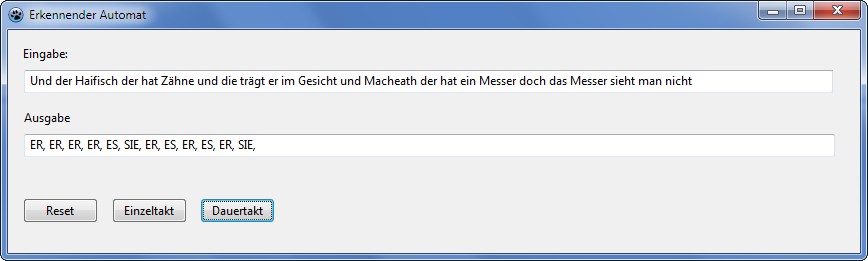
1. Schiffe in Seenot senden SOS. Unser Automat soll aus einer
Zeichenfolge die Notruffolge W...---...W erkennen. Das W soll ein
Worttrennzeichen symbolisieren.
2. Ein erkennender Automat soll gleichzeitig nach den Begriffen ER, SIE
und ES suchen.
3. Gesucht ist ein erkennender Automat, der Dualzahlen erkennt, die eine
ungerade Anzahl von Einsen enthalten.
Im Unterschied zu den Mealy-Automaten des vorherigen Kapitels
verfügen erkennende Automaten über keine Ausgabe. Sie akzeptieren und
erkennen die Eingabe und signalisieren durch ihren Zustand das Ergebnis
nach außen. In der Regel werden Symbole (Buchstaben) als Eingabe
benutzt. Mathematisch wird er durch das folgende 5-Tupel (Σ, S, s0, δ,
F) beschrieben, wobei gilt:
Σ ist das Eingabealphabet (eine endliche nicht leere Menge von
Symbolen),
S ist eine endliche nicht leere Menge von Zuständen,
s0 ist der Anfangszustand und ein Element aus S,
δ ist die Zustandsübergangsfunktion: δ: S x Σ → S,
F ist die Menge von Endzuständen und eine (möglicherweise leere)
Teilmenge von S.
Beispiel 1 SOS:
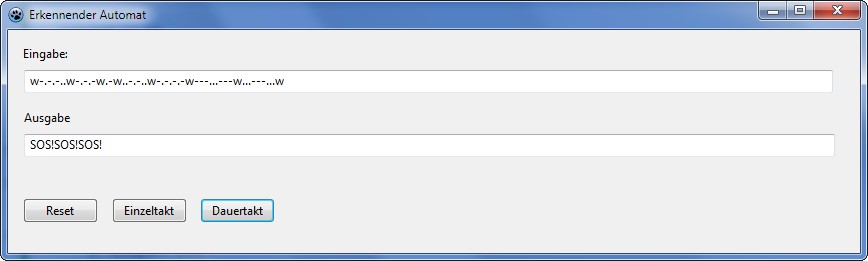
Beispiel 2 ER SIE ES:
(zur besseren Übersicht sind alle anderen Buchstaben ausgelassen worden)

Beispiel 3: