Qualifikationsphase 2
Endliche Automaten mit Ausgabe
Der BCD-Code (von engl. Binary Coded Decimal) bezeichnet in der Informatik in der Regel den 8-4-2-1-Code. In diesem Fall kann Binary Coded Decimal mit dualkodierte Dezimalziffer übersetzt werden. Es handelt sich dann um einen numerischen Code, der jede Ziffer einer Dezimalzahl einzeln dualkodiert. Die Ziffernfolge 8-4-2-1 steht dabei für die Werte der Stellen in einer dualkodierten Dezimalziffer.
Um eine Zahl als BCD-Zahl darzustellen, wird jede dezimale Ziffer (0 bis 9) durch jeweils vier Bit dargestellt (0000 bis 1001). Die verbleibenden sechs Werte (1010 bis 1111), die mit vier Bit darstellbar sind, stellen keine gültigen BCD-Zahlen dar und werden auch als Pseudotetraden bezeichnet.
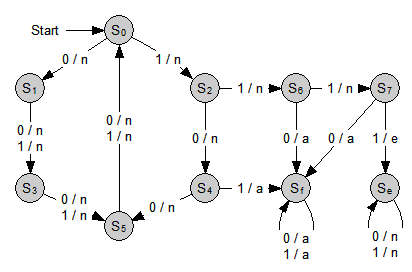
Auf einer einzigen Leitung sollen natürliche Zahlen als BCD-Ziffern gesendet werden. Tritt eine der Pseudotitraden auf, wird ein Fehler gemeldet und die Verbindung geht in einen Fehlerzustand. Einzig die Tetrade 1111 soll dazu neutzt werden, das Ende der Übertragung anzuzeigen.
Zur Lösung des Problems nutzt man Transitionsgraphen oder Zustandsdiagramme. Jeder Zustand wird durch einen Kreis symbolisiert und bildet einen Knoten im Graphen. Von jedem Knoten führen Kanten zu einem oder mehreren anderen Knoten. Auf oder neben dem Knoten werden die Eingaben und die daraus reslutierenden Ausgaben angeschrieben. Der Anfangszustand wird durch einen kleinen Pfeil markiert.
Ein Automat heißt endlich, wenn sowohl die Menge der Zustände, die er annehmen kann (später S genannt), die Menge der möglichen Eingabezeichen und die Menge der möglichen Ausgabezeichen endlich sind.
Die Reaktion des Automaten auf das jeweilige Eingabezeichen wird durch zwei Funktionen festgelegt: die Überführungsfunktion u bestimmt aus Eingabezeichen und Zustand den Folgezustand, die Ausgabefunktion g bestimmt aus Eingabezeichen und Zustand das Ausgabezeichen.
Mathematisch wird der endliche Automat durch ein 7-Tupel (Σ, Γ, S,
s0, δ, ω,F) beschrieben, wobei:
Σ ist das Eingabealphabet (eine endliche nicht leere Menge von
Symbolen),
Γ ist das Ausgabealphabet (eine endliche nicht leere Menge von
Symbolen),
S ist eine endliche nicht leere Menge von Zuständen,
s0 ist der Anfangszustand und ein Element aus S,
δ ist die Zustandsübergangsfunktion: δ: S x Σ → S,
ω ist die Ausgabefunktion: ω: S x Σ → Γ,
F ist die Menge von Endzuständen und eine (möglicherweise leere)
Teilmenge von S.
Falls die Ausgabefunktion eine Funktion von Zustand und Eingabealphabet
ist (ω: S x Σ → Γ), dann handelt es sich um ein Mealy-Modell. Falls die
Ausgabefunktion nur vom Zustand abhängt (ω: S → Γ), dann ist es ein
Moore-Modell.
| Automaton | ||||||||
|