Baumstrukturen

EducETH stellt Unterrichtsmaterialien zu verschiedenen Fächern und Themen zu Verfügung. Der folgende Link (Bäume) führt zu einer Einführung zum Thema "Bäume in der Informatik", der Link (SuchBäume) zu einer EInführung zum Thema "Binäre Suchbäume".

Bäume gehören zu den bedeutendsten Datenstrukturen in der Informatik. Sie werden nicht nur zur effizienten Speicherung und schnellem Finden von Daten benutzt, sondern sind auch ein nützliches Hilfsmittel zur Strukturierung von Informationen. Auch die visuelle Aussagekraft der Bäume wird in den verschiedensten Bereichen eingesetzt. Eine bekannte Datenstruktur ist beispielsweise der Stammbaum. In diesem wird auf jeder Stufe eine Generation dargestellt. Zur Darstellung werden zwei Arten von Stammbäumen benutzt. Der eine weist alle Vorfahren einer Person aus: Auf der ersten Generationsstufe steht die Person, in der zweiten Stufe die Eltern, in der dritten die Großeltern usw. Die Eltern stehen unter den Kindern. Der zweite ist genau anders herum aufgebaut. Die Eltern befinden sich immer über den Kindern. Beide Bäume unterscheiden sich jedoch: im ersten Baum hat jede Person genau zwei Vorfahren, d.h. jede Person verweist auf zwei weitere. In der ersten Generation gibt es 2⁰ (1) Personen, in der zweiten 2¹ (2), in der dritten 2² (4), in der vierten 2³ (8) usw. Im zweiten Baum kann die Anzahl der Nachfahren beliebig sein: sie kann von Null bis unendlich gehen (theoretisch!!!). Der erste Baum wird deshalb auch als Binärbaum bezeichnet.

Bäume in der Informatik bestehen aus Elementen, die eine baumartige Beziehung untereinander haben. Diese Elemente werden als Knoten bezeichnet. Bei einem Stammbaum entspricht jede Person einem Knoten. Alle Knoten bis auf einen haben einen Vorfahren. Dieser eine Knoten
ohne Vorfahren ist die Wurzel. Die Wurzel wird, wie beim Stammbaum, aus praktischen Gründen als oberster Knoten dargestellt. Alle direkten Nachfolger der Wurzel sind die Kinder (Söhne!!!) der Wurzel. Der Vorfahre eines Knoten wird Vater genannt. Die Verbindungen zwischen den Knoten heißen Kanten. Jeder Stammbaum ist endlich. Das heisst, es gibt immer Personen die keine Kinder haben. Das gleiche gilt auch für die Bäume in der Informatik. Ein Knoten, der keinen Nachfolger hat, wird wie beim Baum Blatt genannt. Damit gibt es drei verschiedene Arten von Knoten: die Wurzel, das Blatt und den inneren Knoten. Die maximale Anzahl der direkten Nachfolger, die ein Knoten hat, heißt Grad des Baumes. Ein Binärbaum hat den Grad 2. Die Anzahl der Knoten an dem längsten Pfad heißt Höhe oder Tiefe des Baumes.

Wie schon mehrfach unterschwellig erwähnt, spielt der Binärbaum in der Informatik eine große Rolle. Ein Binärbaum ist ein Baum vom Grad 2. Somit hat jeder Knoten höchstens zwei Söhne. Durch diese Einschränkung vereinfachen sich viele Algorithmen und die visuelle Darstellung der Bäume. Der Binärbaum wird in der Informatik daher oft eingesetzt und liefert die Grundlage für weitere spezialisiertere Bäume. In einem Binärbaum der Tiefe n lassen sich höchstens 2ⁿ-1 Knoten unterbringen. Bei einem unvollständigen Baum sind es entsprechend weniger. Im ungünstigsten Fall lassen sich nur n Knoten unterbringen. Jeder Knoten hat dann genau einen Nachfolger. Dieser Baum wäre dann eine Liste.

Rekursive Beschreibung des Binärbaums: Ein Binärbaum ist entweder leer oder er besteht aus einer Wurzel oder er besteht aus einer Wurzel, die über bis zu zwei Kanten mit disjunkten, nicht leeren Binärbäumen verbunden ist.

Wenn die Knoten untereinander keine Ordnung besitzen, ist der Baum ungeordnet. Bei geordneten Bäumen besteht eine vollständige Ordnungsrelation zwischen den Knoten.

Für viele Anwendungen ist es ausserdem notwendig alle Knoten eines Baumes der Reihe nach zu bearbeiten. Da die Knoten jedoch nicht linear angeordnet sind wie zum Beispiel in einer Liste, gibt es verschiedene Durchlaufordnungen (Traversierung), um alle Knoten eines Baumes zu durchlaufen. Für das Durchlaufen von Binärbäumen sind drei Reihenfolgen von besonderer Bedeutung: die Preorder- (Hauptreihenfolge), die Postorder- (Nebenreihenfolge) und die Inorder-Reihenfolge (symmetrische Reihenfolge). Die Bezeichnungen Preorder, Postorder und Inorder verdeutlichen, ob ein Knoten vor, nach oder zwischen seinen Teilbäumen besucht wird. Die Reihenfolgen können auf einfache Weise rekursiv formuliert werden.

Die Klasse TBinTree

Mit Hilfe der Klasse TBinTree können beliebig viele Inhaltsobjekte in einem Binärbaum verwaltet werden. Ein Objekt der Klasse stellt entweder einen leeren Baum dar oder verwaltet ein Inhaltsobjekt sowie einen linken und einen rechten Teilbaum, die ebenfalls Objekte der Klasse TBinTree sind.

Dokumentation der Klasse TBinTree

Konstruktor	constructor create	Nach dem Aufruf des Konstruktors existiert ein leerer Binärbaum.
Konstruktor	create(pObject: TObject)	Wenn der Parameter pObject ungleich nil ist, existiert nach dem Aufruf des Konstruktors der Binärbaum und hat pObject als Inhaltsobjekt und zwei leere Teilbäume. Falls der Parameter nil ist, wird ein leerer Binärbaum erzeugt.
Konstruktor	create(pObject: TObject;pLeftTree, pRightTree: TBinNaum)	Wenn der Parameter pObject ungleich nil ist, wird ein Binärbaum mit pObject als Inhaltsobjekt und den beiden Teilbäume pLeftTree und pRightTree erzeugt. Sind pLeftTree oder pRightTree gleich nil, wird der entsprechende Teilbaum als leerer Binärbaum eingefügt. Wenn der Parameter pObject gleich nil ist, wird ein leerer Binärbaum erzeugt.
Anfrage	function isEmpty: boolean	Diese Anfrage liefert den Wahrheitswert true, wenn der Binärbaum leer ist, sonst liefert sie den Wert false.
Auftrag	procedure setRootItem(pObject: TObject)	Wenn der Binärbaum leer ist, wird der Parameter pObject als Inhaltsobjekt sowie ein leerer linker und rechter Teilbaum eingefügt. Ist der Binärbaum nicht leer, wird das Inhaltsobjekt durch pObject ersetzt. Die Teilbäume werden nicht geändert. Wenn pObject nil ist, bleibt der Binärbaum unverändert.
Anfrage	function getRootItem: TObject	Diese Anfrage liefert das Inhaltsobjekt des Binärbaums. Wenn der Binärbaum leer ist, wird nil zurückgegeben.
Auftrag	procedure AddTreeLeft(pTree: TBinTree)	Wenn der Binärbaum leer ist, wird pTree nicht angehängt. Andernfalls erhält der Binärbaum den übergebenen Baum als linken Teilbaum. Falls der Parameter nil ist, ändert sich nichts.
Auftrag	procedure addTreeRight(pTree: TBinTree)	Wenn der Binärbaum leer ist, wird pTree nicht angehängt. Andernfalls erhält der Binärbaum den übergebenen Baum als rechten Teilbaum. Falls der Parameter nil ist, ändert sich nichts.
Anfrage	function getLeftTree: TBinTree	Diese Anfrage liefert den linken Teilbaum des Binärbaumes. Der Binärbaum ändert sich nicht. Wenn der Binärbaum leer ist, wird nil zurückgegeben.
Anfrage	function getRightTree: TBinTree	Diese Anfrage liefert den rechten Teilbaum des Binärbaumes. Der Binärbaum ändert sich nicht. Wenn der Binärbaum leer ist, wird nil zurückgegeben.
Destruktor	destructor destroy	Das Objekt der Klasse TBinTree wird entfernt und der von dem Objekt verwendete Speicher wird wieder frei gegeben.
Auftrag	clear	Löschen

TBinTree = class
private
pLeftTree, pRightTree: TBinTree;
pInhalt: TObject;
public
constructor create; overload;
constructor create (pObject: TObject); overload;
constructor create (pObject: TObject; pLeftTree1, pRightTree1: TBinTree); overload;
function isEmpty: Boolean;
procedure clear;
procedure setRootItem (pObject: TObject);
function getRootItem: TObject;
procedure addTreeLeft (pTree: TBinTree);
procedure addTreeRight (pTree: TBinTree);
function getLeftTree: TBinTree;
function getRightTree: TBinTree;
destructor destroy;
end;

Der Stammbaum

hfgh

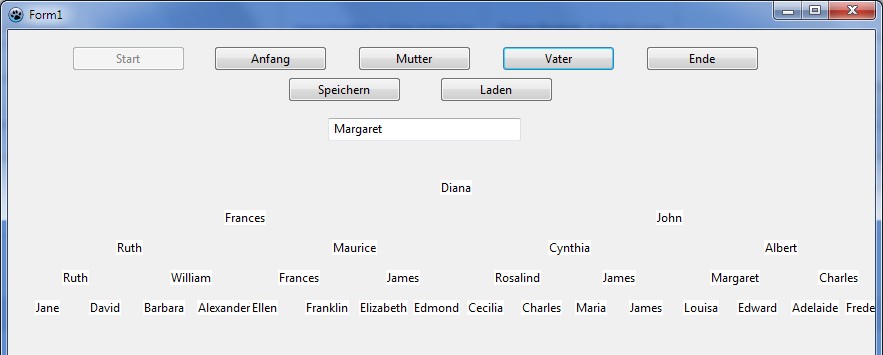
Der Wissensbaum

Wie kann man einen Begriff, den sich eine andere Person ausgedacht hat, möglichst elegant erraten? Diese Fragestellung führt zum grundsätzlichen Problem, wie Frage- und Auskunftssysteme prinzipiell funktionieren.

Das Programm zum Städteraten versucht, eine Stadt, die man sich gemerkt hat, zu erraten. Zunächst sind die Städte Aachen, Stuttgart, Hamburg, Koblenz, Köln und Freiburg in der Datei zum Rateprogramm enthalten.
- Nach welchem Prinzip versucht das Programm, eine Stadt zu raten? Welche Fragetechnik wird dabei benutzt?
- In welchem logischen Zusammenhang stehen die zu ratenden Städtenamen?
- Wie reagiert das Programm, wenn man eine Stadt erfragen lässt, die nicht in der Datei vorhanden ist (z.B. Essen)?

Das Rateproblem

gfgh

Suchbaum und Wörterbuch

Ein Suchbaum unterscheidet sich von einem beliebigen Binärbaum dadurch, dass die Knoten des Suchbaums jederzeit gemäß dem vorhandenen Ordnungskriterium sortiert sind. Der linke Sohn ist stets kleiner als der Vater, der rechte Sohn stets größer oder umgekehrt.Alle Methoden, die die Ordnung des Suchbaums zerstören, sind verboten. Das Einfügen, das Suchen und das Ausgeben von Elementen erfolgt gemäß der vorhandenen Sortierung. Neue Knoten werden immer als Blätter eingefügt. Alle vorhandenen Knoten behalten ihre Position, da sonst die Ordnung verloren geht. Durchläuft man den Suchbaum nach dem Inorder-Verfahren, erhält man alle Knoten in sortierter Reihenfolge. Beim Löschen sind verschiedene Situationen zu berücksichtigen: Blätter werden gelöscht, indem man sie aus dem Suchbaum entfernt. Knoten mit einem leeren Teilbaum werden gelöscht, indem der andere, nicht-leere Teilbaum nachgezogen wird. Knoten mit 2 nicht-leeren Teilbäumen werden gelöscht, indem der zu löschende Knoten durch den nächst kleineren oder den nächst größeren Knoten ersetzt wird. Der nächste kleinere (größere) Knoten hat mindestens einen leeren Teilbaum.

V.Berg • Bergisch Gladbach • Impressum • Haftungsausschluss