Normalformen beschreiben beliebige Funktionen in einheitlicher Form. In der
Boole’schen Algebra sind zwei Normalformen gebräuchlich: die disjunktive
Normalform (DNF) und konjunktive Normalform (KNF).
Beispiel 1: Zur Trinkwasserversorgung eines
Hochhauses ist auf dem Dach ein Vorratsbehälter installiert. Das Wasser wird
durch eine Hauptpumpe bzw. bei deren versagen durch eine Reservepumpe in den
Vorratsbehälter gepumpt. Zur automatischen Steuerung der Pumpen sind an diesen
und an dem Behälter Sensoren angebracht, die melden, wenn dieser nicht mehr
ausreichend gefüllt ist bzw. die Pumpen defekt sind. Es ist ein Schaltnetz zur
Steuerung der Pumpen zu entwickeln; es soll ein Alarmsignal ausgegeben werden,
wenn beide Pumpen defekt sind.
1. Aufstellen der Wahrheitstabelle der gesuchten
Schaltung
Die Eingangsvariable a steht für den Vorratsbehälter (0 = leer,
1 = gefüllt), b für die Hauptpumpe (0 = defekt, 1 = in Ordnung) und c für die
Reservepumpe (0 = defekt, 1 = in Ordnung). Die Ausgangsvariable h steht für die
eingeschaltete Hauptpumpe (h = 1), r für die eingeschaltete Reservepumpe (r = 1)
und s für Alarm ( s = 1). Die Tabelle sieht dann wie folgt aus:
| a |
b |
c |
h |
r |
s |
| 0 |
0 |
0 |
0 |
0 |
1 |
| 0 |
0 |
1 |
0 |
1 |
0 |
| 0 |
1 |
0 |
1 |
0 |
0 |
| 0 |
1 |
1 |
1 |
0 |
0 |
| 1 |
0 |
0 |
0 |
0 |
1 |
| 1 |
0 |
1 |
0 |
0 |
0 |
| 1 |
1 |
0 |
0 |
0 |
0 |
| 1 |
1 |
1 |
0 |
0 |
0 |
2. Die Schaltfunktionen
Für r lässt sich leicht ablesen, dass r den Wert 1 hat, wenn a=0,
b=0 und c=1 ist. Bei einer UND-Verknüpfung müssen alle Variablen den
Wert 1 haben, damit die Verknüpfung ebenfalls den Wert 1 hat. Es
gilt also: r = ¬a ∧ ¬b ∧ c. Für h gibt es zwei Terme: h = t1 ∨ t2.
t1 = ¬a ∧ b ∧ ¬c und t2 = ¬a ∧ b ∧ c. Für h ergibt sich damit der
folgende Term: h = (¬a ∧ b ∧ ¬c) ∨ (¬a ∧ b ∧ c). Nach dem
Distributivgesetz gilt a ∨ (b ∧ c) = (a ∨ b) ∧ (a ∨ c) bzw. (a ∨ b)
∧ (a ∨ c) = a ∨ (b ∧ c). Der Ausdruck ¬a ∧ b lässt sich ausklammern.
Man erhält dann h = (¬a ∧ b) ∨ (c ∧ ¬c). Da c ∧ ¬c = 0 (Komplement)
gilt h = (¬a ∧ b) ∨ 0. Nach dem Null-Theorem ergibt sich daraus h =
¬a ∧ b.
Für s lassen sich ebenfalls zwei Terme bestimmen: s = t1 ∨ t2 = (¬a
∧ ¬b ∧ ¬c) ∨ (a ∧ ¬b ∧ ¬c). Daraus ergibt sich analog der oberen
Rechnung für s = ¬b ∧ ¬c.
3. Die Schaltung
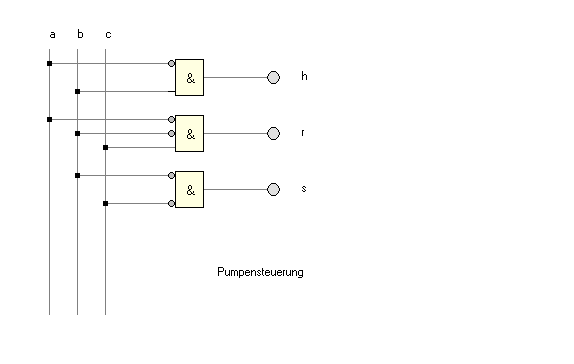
Beispiel 2: Aufzugssteuerung
In einem Gebäude mit acht Stockwerken gibt es mehrere Aufzüge.
Einer davon soll die Eingangshalle und die Stockwerke 4 – 7
miteinander verbinden. Die Stockwerkszahl steht als dreistellige
Dualziffer zur Verfügung.
1. Schaltwerttabelle:
Die Stockwerke werden von durch drei Dualziffern a, b und c
gekennzeichnet. s ist das gesuchte Stockwerk.
| a |
b |
c |
s |
| 0 |
0 |
0 |
1 |
| 0 |
0 |
1 |
0 |
| 0 |
1 |
0 |
0 |
| 0 |
1 |
1 |
0 |
| 1 |
0 |
0 |
1 |
| 1 |
0 |
1 |
1 |
| 1 |
1 |
0 |
1 |
| 1 |
1 |
1 |
1 |
2. Schaltfunktionen
Wie in Beispiel 1 könnte man jetzt alle Terme, für die s = 1 ist,
disjunktiv verknüpfen. Man kann aber alle Terme benutzen, für die s
= 0 ist. Für s gilt dann s = t1 ∧ t2 ∧ t3. Die Terme werden
konjunktiv verknüpft. Damit t1 den Wert 0 annimmt, gilt t1 = a ∨b
∨¬c; für t2 gilt t2 = a ∨¬b ∨c und für t3 gilt t3 = a ∨ ¬b ∨¬c.
Für s ergibt sich dann die folgende Funktion:
s = (a ∨ b ∨ ¬c) ∧ (a ∨ ¬b ∨ c) ∧ (a ∨ ¬b ∨ ¬c)
= a ∨ [( (b ∨ ¬c) ∧ (¬b ∨ c) ∧ (¬b ∨ ¬c)]
= a ∨ [( (b ∨¬c) ∧ ¬b]
= a ∨ [( b ∧ ¬b)∨ ¬c ∧ ¬b)]
= a ∨ (¬b ∧ ¬c).
3. Die Schaltung
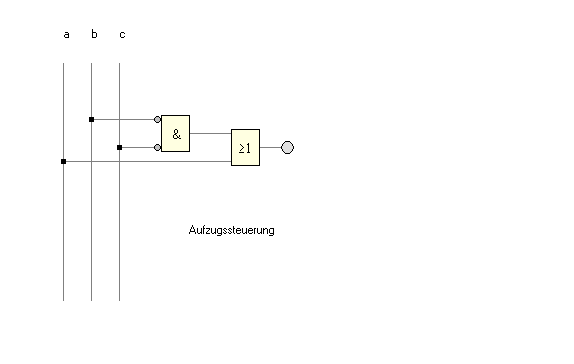
Das folgende Verfahren liefert also die Schaltungssynthese:
1. Aufstellen der Wahrheitstabelle der gesuchten Schaltung
2. Ablesen einer Normalform: Treten als Werte weniger Einsen als
Nullen auf, nehme man die disjunktive (DNF), andernfalls die
konjunktive (KNF) Normalform.
2.1 DNF: Man bildet zu allen Zeilen der Wertetabelle, denen eine 1
zugeordnet ist, die Vollkonjunktion; dabei treten die mit 0 belegten
Variablen negiert auf. Diese Vollkonjunktionen werden disjunktiv
verknüpft.
2.2 KNF: Man bildet zu allen Zeilen der Wertetabelle, denen eine 0
zugeordnet ist, die Volldisjunktion; dabei treten die mit 1 belegten
Variablen negiert auf. Diese Vollkonjunktionen werden konjunktiv
verknüpft.
3. Vereinfachung mittels Boole’scher Algebra.
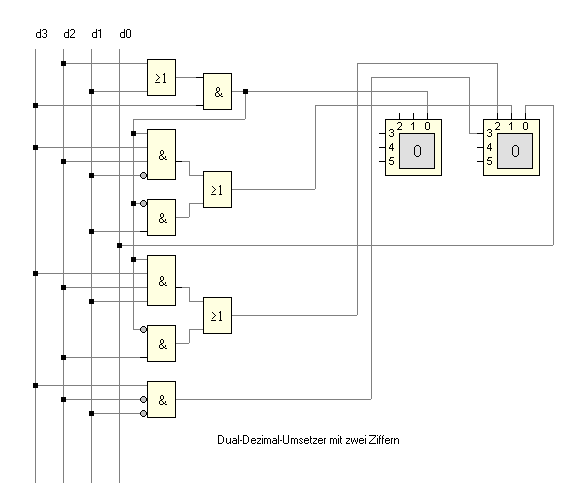
Beispiel 3:Dual-Dezimal-Umsetzer
Eine vierstellige Dualzahl soll in die entsprechende Dezimalzahl
umgesetzt werden. Dazu geht auf vier Leitungen die Dualdarstellung
einer Zahl in die Schaltung ein, während fünf von der Schaltung
ausgehende Leitungen eine zweistellige Dezimalanzeige steuern. Für
die Zehnerziffer Z genügt ein Bit, da aufgrund der vierstelligen
Dualzahl Dezimalzahlen von 0 bis 15 darstellbar sind; d.h., die
Zehnerziffer kann den Wert 0 oder 1 annehmen
| d3 |
d2 |
d1 |
d0 |
Z |
e3 |
e2 |
e1 |
e0 |
| 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
| 0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
| 0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
| 0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
| 0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
| 0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
| 0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
| 1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
| 1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
| 1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
| 1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
| 1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
| 1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
| 1 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
| 1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
Für Z = 1 stehen 6 Terme zur Verfügung. Es gilt also:
Z = (d3 ∧¬d2 ∧d1 ∧¬d0) ∨ (d3 ∧¬d2 ∧d1 ∧d0)∨ (d3 ∧d2 ∧¬d1 ∧¬d0) ∨
(d3 ∧d2 ∧¬d1 ∧d0) ∨ (d3 ∧d2 ∧d1 ∧¬d0)∨ (d3 ∧d2 ∧d1 ∧d0)
= d3 ∧ [(¬d2 ∧d1 ∧¬d0) ∨ (¬d2 ∧d1 ∧d0)∨ (d2 ∧¬d1 ∧¬d0) ∨ (d2
∧¬d1 ∧d0) ∨ (d2 ∧d1 ∧¬d0)∨ (d2 ∧d1 ∧d0)]
= d3 ∧ [[(¬d2 ∧d1 ∧¬d0) ∨ (¬d2 ∧d1 ∧d0)]∨ [(d2 ∧¬d1 ∧¬d0) ∨ (d2
∧¬d1 ∧d0)] ∨ [(d2 ∧d1 ∧¬d0)∨ (d2 ∧d1 ∧d0)]]
= d3 ∧ [[(¬d2 ∧d1) ∧ (¬d0 ∨d0)]∨ [(d2 ∧¬d1)∧ (¬d0 ∨d0)] ∨ [(d2
∧d1) )∧ (¬d0 ∨d0)]]
= d3 ∧ [[(¬d2 ∧d1) ∧ 1]∨ [(d2 ∧¬d1)∧ 1] ∨ [(d2 ∧d1)∧ 1]]
= d3 ∧ [(¬d2 ∧d1) ∨ (d2 ∧¬d1) ∨ (d2 ∧d1)]
= d3 ∧ [(¬d2 ∧d1) ∨ [(d2 ∧d1)∨ (d2 ∧ ¬d1)]]
= d3 ∧ [(¬d2 ∧d1) ∨ [d2 ∧(d1 ∨¬d1)]]
= d3 ∧ [(¬d2 ∧d1) ∨ (d2 ∧1)]
= d3 ∧ [(¬d2 ∧d1) ∨ d2]
= d3 ∧ [(¬d2∨ d2) ∧ d1 ∨ d2)]
= d3 ∧ [1 ∧ d1 ∨ d2)]
= d3 ∧ (d1 ∨ d2)
Der Rechenaufwand, der hier betrieben wurde, ist sehr aufwändig.
Wie Boole’sche Funktionen recht einfach minimiert werden können,
zeigt der nächste Abschnitt. Die Funktionen für die anderen Werte
können mit etwas Überlegung aus der Wahrheitswertetabelle
ermittelt werden:
e0: Da die Werte für e0 und d0 identisch sind, gilt e0=d0.
e1: Solange Z=0 ist, entsprechen sich die Werte von d1 und e1.
Wenn Z=1 ist, haben d3 und d2 den Wert 1 und d1 den Wert 0. e1
ist also e1=1, wenn Z=0 und d1 = 1 ist oder wenn Z=0 und d3=1,
d2=1 und d1=0 sind. Die Funktion lautet dann:
e1=( ¬Z ∧d1)∨ (Z ∧d3 ∧d2 ∧ ¬d1).
e2: Für e2 gelten ähnliche Überlegungen. Die Funktion für e2
lautet:
e2 = ( ¬Z ∧ d2) ∨ (Z ∧ d3 ∧ d2 ∧ d1).
e3: Diese Funktion soll noch einmal algebraisch hergeleitet
werden.
e3 = (d3 ∧ ¬d2 ∧ ¬d1 ∧ ¬d0) ∨ (d3 ∧ ¬d2 ∧ ¬d1 ∧ d0)
= (d3 ∧ ¬d2 ∧ ¬d1) ∧ (¬d0 ∨ d0)
= (d3 ∧ ¬d2 ∧ ¬d1)∧ 1
= d3 ∧ ¬d2 ∧ ¬d1.
Verfahren von Quine und McCluskey
Die algebraische Ermittlung der Funktionen kann sehr aufwändig
sein. Das im Folgenden vorgestellte Verfahren erleichtert die
Bestimmung von komplexen Funktionen.
1. Ermittlung aller Minterme (Wert der Zielvariablen gleich 1) der
Funktionen.
2. Zusammenfassung der Minterme in Gruppen mit gleicher Anzahl
negativer Eingangsvariablen (gleicher Anzahl von Nullen).
3. Wenn es möglich ist, werden Terme benachbarter Gruppen paarweise
zusammengefasst. Terme, die zusammengefasst werden, werden
gekennzeichnet.
4. Schritt 3 wird solange wiederholt, bis keine Vereinfachung mehr
möglich ist.
5. Ermittlung der Kernimplikanten aus den gefundenen Priminplikanten.
Die Kernimplikanten gehören auf jeden Fall zur gesuchten Funktion.
6. Hinzufügen von Kernimplikanten zur Funktion, bis alle Minterme
berücksichtigt sind.
7. Erstellen der Primtermtabelle
8. Dominanzprüfung (Spaltendominanz- und Zeilendominanz)
Das Verfahren wird anhand des Beispiels 3 näher erläutert. Die
Funktion für Z wurde oben algebraisch berechnet. Das Ergebnis war Z
= d3 ∧ (d1 ∨ d2). Zu demselben Ergebnis sollte auch das Verfahren
von Quine und McCluskey kommen. Die folgende Tabelle stellt einen
Ausschnitt aus der Wahrheitstabelle ergänzt um die Spalten Minterm
und Gruppe dar. Die Punkte 7 und 8 kommen hier nicht zur Anwendung,
da das Ergebnis bereits vorher klar ist. In einem weiteren Beispiel
werden sie aber berücksichtigt.
| d3 |
d2 |
d1 |
d0 |
Z |
MinTerm |
Gruppe |
| 0 |
0 |
0 |
0 |
0 |
|
|
| 0 |
0 |
0 |
1 |
0 |
|
|
| 0 |
0 |
1 |
0 |
0 |
|
|
| 0 |
0 |
1 |
1 |
0 |
|
|
| 0 |
1 |
0 |
0 |
0 |
|
|
| 0 |
1 |
0 |
1 |
0 |
|
|
| 0 |
1 |
1 |
0 |
0 |
|
|
| 0 |
1 |
1 |
1 |
0 |
|
|
| 1 |
0 |
0 |
0 |
0 |
|
|
| 1 |
0 |
0 |
1 |
0 |
|
|
| 1 |
0 |
1 |
0 |
1 |
m10 |
2 |
| 1 |
0 |
1 |
1 |
1 |
m11 |
1 |
| 1 |
1 |
0 |
0 |
1 |
m12 |
2 |
| 1 |
1 |
0 |
1 |
1 |
m13 |
1 |
| 1 |
1 |
1 |
0 |
1 |
m14 |
1 |
| 1 |
1 |
1 |
1 |
1 |
m15 |
0 |
Die Minterme ergeben sich aus der konjunktiven Verknüpfung. Zur
Erläuterung und zum einfacheren Bearbeiten sind die entsprechenden
Dualzahlen unterhalb der Minterme aufgeführt. Da vier Eingangswerte
vorliegen, wird eine vierstellige Dualzahl benutzt. In der 1.
Vereinfachung werden Minterme paarweise zusammengefasst. Dazu müssen
die Minterme in mindestens drei Positionen identisch sein. Die
vierte Stelle fällt weg (In den Dualzahlen taucht dafür ein Strich
auf.). In der zweiten Vereinfachung werden die Ergebnisse der 1.
Vereinfachung auch wieder paarweise bearbeitet. Eine weitere
Vereinfachung ist dem vorgegebenen Beispiel nicht möglich. Alle
Terme, die nicht zur Vereinfachung benutzt wurden bzw. nicht mehr
weiter vereinfacht werden können, werden konjunktiv zusammengefasst.
| Minterme |
|
1. Vereinfachung |
|
2. Vereinfachung |
| Gruppe 0 |
|
m15=d3 ∧ d2 ∧ d1 ∧ d0
1111
|
x |
I1,0=m15 ∨ m14
= d3 ∧ d2 ∧ d1
1111
1110
111-
I1,1=m15 ∨ m13
= d3 ∧ d2 ∧ d0
1111
1101
11-1
I1,2=m15 ∨ m11
= d3 ∧ d1 ∧ d0
1111
1011
1-11 |
x
x
x |
I2,0=I1,0 ∨ I1,5
= d3 ∧ d2
111-
110-
11--
I2,1=I1,0 ∨ I1,6
= d3 ∧ d1
111-
101-
1-1-
I2,2=I1,1 ∨ I1,3
= d3 ∧ d2
11-1
11-0
11--
I2,3=I1,2 ∨ I1,4
= d3 ∧ d1
1-11
1-10
1-1-
|
| Gruppe 1 |
m14=d3 ∧ d2 ∧ d1 ∧ ¬d0
1110
m13=d3 ∧ d2 ∧ ¬d1 ∧ d0
1101
m11=d3 ∧ ¬d2 ∧ d1 ∧ d0
1011 |
x
x
x |
I1,3=m14 ∨ m12
= d3 ∧ d2 ∧ ¬d0
1110
1100
11-0
I1,4=m14 ∨ m10
= d3 ∧ d1 ∧ ¬d0
1110
1010
1-10
I1,5=m13 ∨ m12
= d3 ∧ d2 ∧ ¬d1
1101
1100
110-
I1,6=m11 ∨ m10
= d3 ∧ ¬d2 ∧ d1
1011
1010
101-
|
x
x
x
x |
|
| Gruppe 2 |
m12=d3 ∧ d2 ∧ ¬d1 ∧ ¬d0
1100
m10=d3 ∧ ¬d2 ∧ d1 ∧ ¬d0
1010 |
x
x |
|
|
|
I2,0 und I2,2 bzw. I2,1 und I2,3 sind identisch. Deshalb werden
I2,2 und I2,3 nicht berücksichtigt. Z berechnet sich aus den nicht
mit x versehenen Termen.
Z =(d3 ∧ d2) ∨ (d3 ∧ d1) = d3 ∧ (d2 ∨ d1).
Es sollen nun auch die Werte für e2 und e1 mit Hilfe des Verfahrens
bestimmt werden. Im Beispiel wurde das Ergebnis durch etwas
Überlegung abgeleitet.
| d3 |
d2 |
d1 |
d0 |
e2 |
MinTerm |
Gruppe |
| 0 |
0 |
0 |
0 |
0 |
|
|
| 0 |
0 |
0 |
1 |
0 |
|
|
| 0 |
0 |
1 |
0 |
0 |
|
|
| 0 |
0 |
1 |
1 |
0 |
|
|
| 0 |
1 |
0 |
0 |
1 |
m4 |
3 |
| 0 |
1 |
0 |
1 |
1 |
m5 |
2 |
| 0 |
1 |
1 |
0 |
1 |
m6 |
2 |
| 0 |
1 |
1 |
1 |
1 |
m7 |
1 |
| 1 |
0 |
0 |
0 |
0 |
|
|
| 1 |
0 |
0 |
1 |
0 |
|
|
| 1 |
0 |
1 |
0 |
0 |
|
|
| 1 |
0 |
1 |
1 |
0 |
|
|
| 1 |
1 |
0 |
0 |
0 |
|
|
| 1 |
1 |
0 |
1 |
0 |
|
|
| 1 |
1 |
1 |
0 |
1 |
m14 |
1 |
| 1 |
1 |
1 |
1 |
1 |
m15 |
0 |
| Minterme |
|
1. Vereinfachung |
|
2. Vereinfachung |
| Gruppe 0 |
|
m15
1111
|
x |
I1,0 = m15 ∨ m14
1111
1110
111-
I1,1 m15 ∨ m7
1111
0111
-111 |
x
x
|
I2,0 = I1,0 ∨ I1,3
111 -
011 -
- 11 -
I2,1= I1,1 ∨ I1,2
- 111
- 110
- 11 -
|
| Gruppe 1 |
m14
1110
m7
0111 |
x
x
|
I1,2 = m14 ∨ m6
1110
0110
-110
I1,3 = m7 ∨ m6
0111
0110
011-
I1,4 = m7 ∨ m5
0111
0101
01-1
|
x
x
x
|
I2,2= I1,3 ∨ I1,6
011-
010-
01--
I2,3 = I1,4 ∨ I1,5
01-1
01-0
01-- |
| Gruppe 2 |
m6
0110
m5
0101 |
x
x |
I1,5 m6 ∨ m4
0110
0100
01-0
I1,6 m5 ∨ m4
0101
0100
010- |
x
x |
|
| Gruppe 3 |
m4
0100 |
x |
|
|
|
e2 = (d2 ∧ d1) ∨ (¬d3 ∧ d2) = d2 ∧ (d1 ∨ ¬d3)
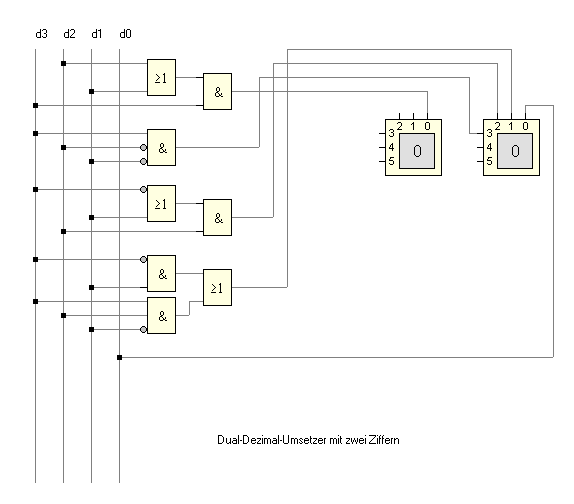
Diese Lösung ist noch eleganter als die Überlegungen aus dem oberen Teil,
unterscheidet sich aber von der vorherigen Lösung. Sie führt aber, wie nachher
aus der Schaltung ersichtlich wird, zum selben Ergebnis.
| d3 |
d2 |
d1 |
d0 |
e1 |
MinTerm |
Gruppe |
| 0 |
0 |
0 |
0 |
0 |
|
|
| 0 |
0 |
0 |
1 |
0 |
|
|
| 0 |
0 |
1 |
0 |
1 |
m2 |
3 |
| 0 |
0 |
1 |
1 |
1 |
m3 |
2 |
| 0 |
1 |
0 |
0 |
0 |
|
|
| 0 |
1 |
0 |
1 |
0 |
|
|
| 0 |
1 |
1 |
0 |
1 |
m6 |
2 |
| 0 |
1 |
1 |
1 |
1 |
m7 |
1 |
| 1 |
0 |
0 |
0 |
0 |
|
|
| 1 |
0 |
0 |
1 |
0 |
|
|
| 1 |
0 |
1 |
0 |
0 |
|
|
| 1 |
0 |
1 |
1 |
0 |
|
|
| 1 |
1 |
0 |
0 |
1 |
m12 |
2 |
| 1 |
1 |
0 |
1 |
1 |
m13 |
1 |
| 1 |
1 |
1 |
0 |
0 |
|
|
| 1 |
1 |
1 |
1 |
0 |
|
|
| Minterme |
|
1. Vereinfachung |
|
2. Vereinfachung |
| Gruppe 1 |
|
m13
1101
m7
0111
|
x
x |
I1,0 =m13 ∨ m12
1101
1100
110 -
I1,1 = m7 ∨ m6
0111
0110
011 -
I1,2 = m7 ∨ m3
0111
0011
0 -11 |
x
x
|
I2,0 = I1,1 Ú I1,4
011 -
001 –
0 -1 -
I2,1 = I1,2 Ú I1,3
0 -11
0 -10
0 -1 -
|
| Gruppe 2 |
m12
1100
m6
0110
m3
0011 |
x
x
x
|
I1,3 = m6 ∨ m2
0110
0010
0-10
I1,4 = m3 ∨ m2
0011
0010
001-
|
x
x
|
|
| Gruppe 3 |
m2
0010 |
x
|
|
|
|
Da I1,0 nicht weiter benutzt wurde, muss dieser Term Bestandteil
der endgültigen Funktion sein. I2,0 und I2,1 sind identisch.
e1 = (d3 ∧ d2 ∧ ¬d1) ∨ (¬d3 ∧ d1)
Ein weiteres Beispiel
1. Ermitteln der Minterme
| d3 |
d2 |
d1 |
d0 |
Y |
MinTerm |
Gruppe |
| 0 |
0 |
0 |
0 |
1 |
m0 |
4 |
| 0 |
0 |
0 |
1 |
1 |
m1 |
3 |
| 0 |
0 |
1 |
0 |
0 |
|
|
| 0 |
0 |
1 |
1 |
0 |
|
|
| 0 |
1 |
0 |
0 |
1 |
m4 |
3 |
| 0 |
1 |
0 |
1 |
1 |
m5 |
2 |
| 0 |
1 |
1 |
0 |
1 |
m6 |
2 |
| 0 |
1 |
1 |
1 |
1 |
m7 |
1 |
| 1 |
0 |
0 |
0 |
1 |
m8 |
3 |
| 1 |
0 |
0 |
1 |
1 |
m9 |
2 |
| 1 |
0 |
1 |
0 |
0 |
|
|
| 1 |
0 |
1 |
1 |
0 |
|
|
| 1 |
1 |
0 |
0 |
0 |
m11 |
2 |
| 1 |
1 |
0 |
1 |
0 |
|
|
| 1 |
1 |
1 |
0 |
0 |
|
|
| 1 |
1 |
1 |
1 |
1 |
m15 |
0 |
Ermitteln der Primterme
| Minterme |
|
1. Vereinfachung |
|
2. Vereinfachung |
| Gruppe 0 |
|
m15=d3 ∧ d2 ∧ d1 ∧ d0
1111
|
x |
I1,0=m15 ∨ m11
= d3 ∧ d1 ∧ d0
1111
1011
1-11
I1,1=m15 ∨ m7
= d2 ∧ d1 ∧ d0
1111
0111
-111
|
P1
P2
|
|
| Gruppe 1 |
m7=¬d3 ∧ d2 ∧ d1 ∧ d0
0111
m11=d3 ∧ ¬d2 ∧ d1 ∧ d0
1011 |
x
x
|
I1,2=m5 ∨ m7
= ¬d3 ∧ d2 ∧ d0
0101
0111
01-1
I1,3=m6 ∨ m7
= ¬d3 ∧ d2 ∧
d1
0110
0111
011-
I1,4=m9 ∨ m11
= d3 ∧ ¬d2 ∧ d0
1001
1011
10-1
|
x
x
P3
|
I2,0=I1,2
∨ I1,7 P4
= ¬d3 ∧ d2
01-1
01-0
01--
I2,1=I1,3 ∨ I1,8
= ¬d3 ∧ d2
011-
010-
01-- |
| Gruppe 2 |
m5=¬d3 ∧ d2 ∧ ¬d1 ∧ d0
0101
m6=¬d3 ∧ d2 ∧ d1 ∧ ¬d0
0110
m9=d3 ∧ ¬d2 ∧ ¬d1 ∧ d0
1001 |
x
x
x |
I1,5=m1 ∨ m5
= ¬d3 ∧ ¬d1 ∧ d0
0001
0101
0-01
I1,6=m1 ∨ m9
= ¬d2 ∧¬ d1 ∧ d0
0001
1001
-001
I1,7=m4 ∨ m6
= ¬d3 ∧ d2 ∧ ¬d0
0100
0110
01-0
I1,8=m4 ∨ m5
= ¬d3 ∧ d2 ∧ ¬d1
0100
0101
010-
1,9=m8 ∨ m9
= d3 ∧ ¬d2 ∧ ¬d1
1000
1001
100- |
x
x
x
x
x
|
I2,2=I1,5 ∨ I1,11
= ¬d3 ∧ ¬d1
0-01
0-00
0-0-
I2,3=I1,6 ∨ I1,12
= ¬d2 ∧ ¬d1
-001
-000
-00-
I2,4=I1,10
∨ I1,8 P5
= ¬d3 ∧ ¬d1
000-
010-
0-0-
I2,5=I1,10
∨ I1,9 P6
= ¬d2 ∧ ¬d1
000-
100-
-00- |
| Gruppe 3 |
m1=¬d3 ∧ ¬d2 ∧ ¬d1 ∧ d0
0001
m4=¬d3 ∧ d2 ∧ ¬d1 ∧ ¬d0
0100
m8=d3 ∧ ¬d2 ∧ ¬d1 ∧ ¬d0
1000 |
x
x
x |
I1,10=m0 ∨ m1
= ¬d3 ∧ ¬d2 ∧ ¬d1
0000
0001
000-
I1,11=m0 ∨ m4
= ¬d3 ∧ ¬d1 ∧ ¬d0
0000
0100
0-00
I1,12=m0 ∨ m8
=
¬d2 ∧ ¬d1 ∧ ¬d0
0000
1000
-000 |
x
x
x |
|
| Gruppe 4 |
m5´0=¬d3 ∧ ¬d2 ∧ ¬d1 ∧ ¬d0
0000
|
x |
|
|
|
Es ergeben sich sechs Primterme. Anhand dieser Terme wird eine Primtermtabelle erstellt
Als erstes wird eine Spaltendominazprüfung durchgeführt. Die Spalten werden paarweise darauf verglichen, ob nicht eine Spalte
existiert, in der die markierten Primterme eine Teilmenge der markierten
Primterme der anderen Spalte sind. Ist dies der Fall, kann die Spalte
mit der Obermege gestrichen werden. In der folgenden
Zeilendominanzprüfung werden die Zeilen paarweise miteinander verglichen.
Existiert eine Zeile, in denen die Minterme einer Teilmenge der Minterme
der anderen Zeile sind, so wird sie gestrichen. Die Relation ist also
umgekehrt zur Spaltendominanzprüfung. Die erste Spaltendominanzprüfung ergibt,
dass m0, m1 und m9 wegen m8 und m4, m5 und m7 wegen m6 gestrichen werden
können. Danach sieht die Tabelle wie folgt aus:
Die Zeilendominanzprüfung ergibt, das P5 (leer), P2 (wegen P1) und P3
(wegen P1) gestrichen werden können.
Eine zweite Spaltendominanzprüfung führt zum Streichen von m15 wegen
m11. Das Ergebnis ist




