Boole'sche Algebra
Als elementare Operatoren dienen üblicherweise die Operatoren
UND, ODER und NICHT (AND, OR, NOT; ∧, ∨, ¬). Es gelten die
folgenden Postulate:
1. ¬a ist genau dann wahr, wenn a falsch ist. Es gilt also ¬0 =
1, ¬1 = 0.
2. a ∧ b ist genau dann wahr, wenn sowohl a als auch b wahr
sind. Es gilt also 0 ∧ 0 = 0 ∧ 1 = 1 ∧ 0 = 0 und 1 ∧ 1 = 1
3. a ∨ b ist genau dann wahr, wenn a oder b wahr sind. Es gilt 0
∨ 0 = 0 und 0 ∨ 1 = 1 ∨ 0 = 1 ∨ 1 = 1
Basierend auf den Postulaten gelten elementare Theoreme:
1. Null- und Eins-Theorem
x ∧ 0 = 0, x ∧ 1 = x, x ∨ 0 = x, x ∨ 1 = 1
2. Indempotenz
x ∧ x = x, x ∨ x = x
3. Komplement
x ∧ ¬x = 0, x ∨ ¬x = 1
Mit Hilfe der Boole’schen Algebra lassen sich logische
Digitalschaltungen entwickeln. NICHT-Gatter besitzen einen
Eingang und einen Ausgang, UND-Gatter und ODER-Gatter haben je
zwei Eingänge. In der Praxis werden meistens Schaltungen mit
mehr als zwei Eingängen benötigt; diese lassen sich aus weiteren
Gattern zusammensetzen.
Es gibt 16 Boole’sche Funktionen mit zwei Eingängen und einem
Ausgang.
|
a
|
0
|
0
|
1
|
1
|
Term
|
Bezeichnung
|
Sprechweise
|
|
b
|
0
|
1
|
0
|
1
|
|
f0
|
0
|
0
|
0
|
0
|
0
|
Nullfunktion
|
|
|
f1
|
0
|
0
|
0
|
1
|
a ∧ b
|
Konjunktion
|
a UND b
|
|
f2
|
0
|
0
|
1
|
0
|
a ∧ ¬b
|
Erste Differenz (Inhibition)
|
a MINUS b
|
|
f3
|
0
|
0
|
1
|
1
|
a
|
Erste Identität
|
|
|
f4
|
0
|
1
|
0
|
0
|
¬a ∧ b
|
Zweite Differenz
|
b MINUS a
|
|
f5
|
0
|
1
|
0
|
1
|
b
|
Zweite Identität
|
|
|
f6
|
0
|
1
|
1
|
0
|
(¬a ∧ b) ∨ (a ∧ ¬b)
|
Antivalenz
|
a XOR b
|
|
f7
|
0
|
1
|
1
|
1
|
a ∨ b
|
Disjunktion
|
a ODER b
|
|
f8
|
1
|
0
|
0
|
0
|
¬(a ∨ b)
|
Negatdisjunktion
|
a NOR b
|
|
f9
|
1
|
0
|
0
|
1
|
(¬a ∨ b) ∧ (a ∨ ¬b)
|
Äquivalenz
|
a XNOR b
|
|
f10
|
1
|
0
|
1
|
0
|
¬b
|
Zweite Negation
|
NICHT b
|
|
f11
|
1
|
0
|
1
|
1
|
a ∨ ¬b
|
Zweite Implikation
|
b IMPLIZIERT a
|
|
f12
|
1
|
1
|
0
|
0
|
¬a
|
Erste Negation
|
|
|
f13
|
1
|
1
|
0
|
1
|
¬a ∨ b
|
Erste Implikation
|
a IMPLIZIERT b
|
|
f14
|
1
|
1
|
1
|
0
|
¬(a ∧ b)
|
Negatkonjunktion
|
a NAND b
|
|
f15
|
1
|
1
|
1
|
1
|
1
|
Einsfunktion
|
|
Die Funktionen f0, f3, f5, f10, f 12 und f15 sind
uninteressant.
| a |
b |
c |
NOR |
|
| 0 |
0 |
1 |
c = ¬ (a ∨ b) |
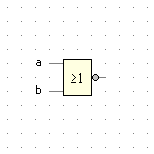
|
| 0 |
1 |
0 |
| 1 |
0 |
0 |
| 1 |
1 |
0 |
| |
|
|
| a |
b |
c |
Inhibition |
|
| 0 |
0 |
0 |
c = a ∧ ¬b |
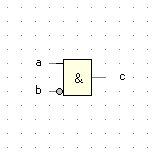
|
| 0 |
1 |
1 |
| 1 |
0 |
0 |
| 1 |
1 |
0 |
| |
|
|
| a |
b |
c |
Inhibition |
|
| 0 |
0 |
0 |
c = ¬a ∧ b |
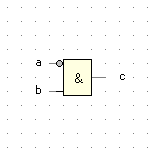
|
| 0 |
1 |
0 |
| 1 |
0 |
1 |
| 1 |
1 |
0 |
| |
|
|
| a |
b |
c |
XOR |
|
| 0 |
0 |
0 |
c = (¬a ∧ b) ∨ (a ∧ ¬b) |
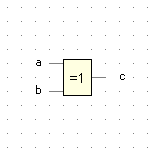
|
| 0 |
1 |
1 |
| 1 |
0 |
1 |
| 1 |
1 |
0 |
| |
|
|
| a |
b |
c |
NAND |
|
| 0 |
0 |
1 |
c = ¬ (a ∧ b) |
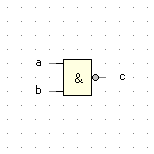
|
| 0 |
1 |
1 |
| 1 |
0 |
1 |
| 1 |
1 |
0 |
| |
|
|
| a |
b |
c |
AND |
|
| 0 |
0 |
0 |
c = a ∧ b |
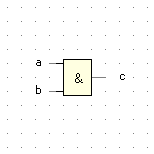
|
| 0 |
1 |
0 |
| 1 |
0 |
0 |
| 1 |
1 |
1 |
| |
|
|
| a |
b |
c |
Äquivalenz |
|
| 0 |
0 |
1 |
c = (¬a ∨ b) ∧ (a ∨ ¬b) |
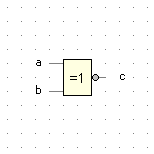
|
| 0 |
1 |
0 |
| 1 |
0 |
0 |
| 1 |
1 |
1 |
| |
|
|
| a |
b |
c |
Implikation |
|
| 0 |
0 |
1 |
c = a ∨ ¬b |
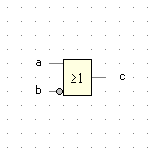
|
| 0 |
1 |
1 |
| 1 |
0 |
0 |
| 1 |
1 |
1 |
| |
|
|
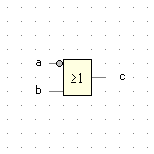
| a |
b |
c |
Implikation |
|
| 0 |
0 |
1 |
c = ¬a ∨ b |
|
| 0 |
1 |
0 |
| 1 |
0 |
1 |
| 1 |
1 |
1 |
| |
|
|
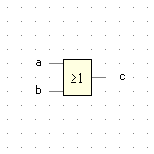
| a |
b |
c |
ODER |
|
| 0 |
0 |
0 |
c = a ∨ b |
|
| 0 |
1 |
1 |
| 1 |
0 |
1 |
| 1 |
1 |
1 |
| |
|
|
Wie in der Algebra gibt es auch in der Schaltalgebra
Rechenregeln.
1. Kommutativgesetz
a ∧ b = b ∧ a
a ∨ b = b ∨ a
2. Assoziativgesetz
(a ∧ b) ∧ c = a ∧ (b ∧ c) = a ∧ b ∧ c = b ∧ a ∧ c = c ∧ a ∧ b =
a ∧ c ∧ b= c ∧ b ∧ a
(a ∨ b) ∨ c = a ∨ (b ∨ c) = a ∨ b ∨ c = b ∨ a ∨ c = c ∨ a ∨ b =
a ∨ c ∨ b = c ∨ b ∨ a
3. Distributivgesetz
a ∧ (b ∨ c) =(a ∧b) ∨ (a ∧ c)
a ∨ (b ∧ c) =(a ∨ b) ∧ (a ∨ c)
4. Kürzungsregeln
a ∨ (a ∧ b) = a
a ∧ (a ∨ b) = a
a ∨ (¬a ∧ b) = a ∨ b
a ∧ (¬a ∨ b) = a ∧ b
(a ∧ b) ∨ (a ∧ ¬b) = a
(a ∨ b) ∧ (a ∨ ¬b) = a
5. De Morgan’sche Gesetze
¬ (a ∧ b) = ¬a ∨ ¬b
¬ (a ∨ b) = ¬a ∧ ¬b
Alle zweistelligen booleschen Funktionen können mit Hilfe der
Negation, der Konjunktion und der Disjunktion dargestellt
werden. Es gilt sogar, dass alle zweistelligen Funktionen mit
Hilfe der Negation und der Konjunktion oder mit Hilfe der
Negation und der Disjunktion dargestellt werden. Betrachtet man
die Negatdisjunktion und die Negatkonjunktion gilt sogar, dass
alle Funktionen entweder mit Hilfe der NAND-Verknüpfung oder der
NOR-Verknüpfung gebildet werden können.

